what proportion of the area under the curve lies to the left of the t= 2.518

three.3.2 - The Standard Normal Distribution

A special instance of the normal distribution has mean \(\mu = 0\) and a variance of \(\sigma^2 = 1\). The 'standard normal' is an important distribution.

Standard Normal Distribution

A standard normal distribution has a mean of 0 and variance of one. This is too known as a z distribution. Yous may see the notation \(N(\mu, \sigma^two\)) where Due north signifies that the distribution is normal, \(\mu\) is the mean, and \(\sigma^2\) is the variance. A Z distribution may be described as \(N(0,one)\). Note that since the standard deviation is the square root of the variance then the standard difference of the standard normal distribution is 1.

The Standard Normal Distribution

Finding Probabilities of a Standard Normal Random Variable Section

As we mentioned previously, calculus is required to notice the probabilities for a Normal random variable.  Fortunately, nosotros have tables and software to aid us.

For whatsoever normal random variable, we tin can transform it to a standard normal random variable by finding the Z-score. Then we can find the probabilities using the standard normal tables.

Almost statistics books provide tables to brandish the surface area under a standard normal curve. Expect in the appendix of your textbook for the Standard Normal Tabular array. We include a similar table, the Standard Normal Cumulative Probability Table so that y'all can print and refer to information technology easily when working on the homework.

Most standard normal tables provide the "less than probabilities".  For instance, if \(Z\) is a standard normal random variable, the tables provide \(P(Z\le a)=P(Z<a)\), for a constant, \(a\).

Example three-9: Probability 'less than' Section

Find the area under the standard normal curve to the left of 0.87.

At that place are 2 main ways statisticians notice these numbers that require no calculus! Click on the tabs below to see how to answer using a table and using engineering science.

• Method 1: Using a table
• Method 2: Using Minitab

A typical four-decimal-place number in the body of the Standard Normal Cumulative Probability Tabular array gives the area under the standard normal curve that lies to the left of a specified z-value. The probability to the left of z = 0.87 is 0.8078 and it tin can be institute by reading the tabular array:

1. Since z = 0.87 is positive, utilise the table for POSITIVE z-values.
2. Go down the left-hand cavalcade, label z to "0.8."
3. And so, go across that row until nether the "0.07" in the acme row.

You should find the value, 0.8078. Therefore,\(P(Z< 0.87)=P(Z\le 0.87)=0.8078\)

z	.00	.01	.02	.03	.04	.05	.06	.07	.08	.09
0.6	.7257	.7291	.7324	.7357	.7389	.7422	.7454	.7586	.7517	.7549
0.7	.7580	.7611	.7642	.7673	.7704	.7734	.7764	.7794	.7823	.7852
0.8	.7881	.7910	.7939	.7967	.7995	.8023	.8051	.8078	.8106	.8133
0.ix	.8159	.8186	.8212	.8238	.8264	.8289	.8315	.8340	.8365	.8389

Using Minitab

To find the area to the left of z = 0.87 in Minitab...

1. From the Minitab card select Calc> Probability Distributions> Normal.
2. Select Cumulative Probability.
3. In the Input constant box, enter 0.87. Click OK

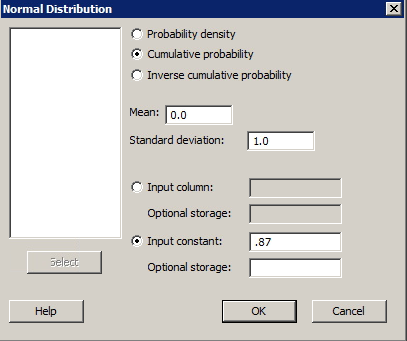
Y'all should encounter a value very close to 0.8078.

Instance 3-10: Probability 'greater than' Department

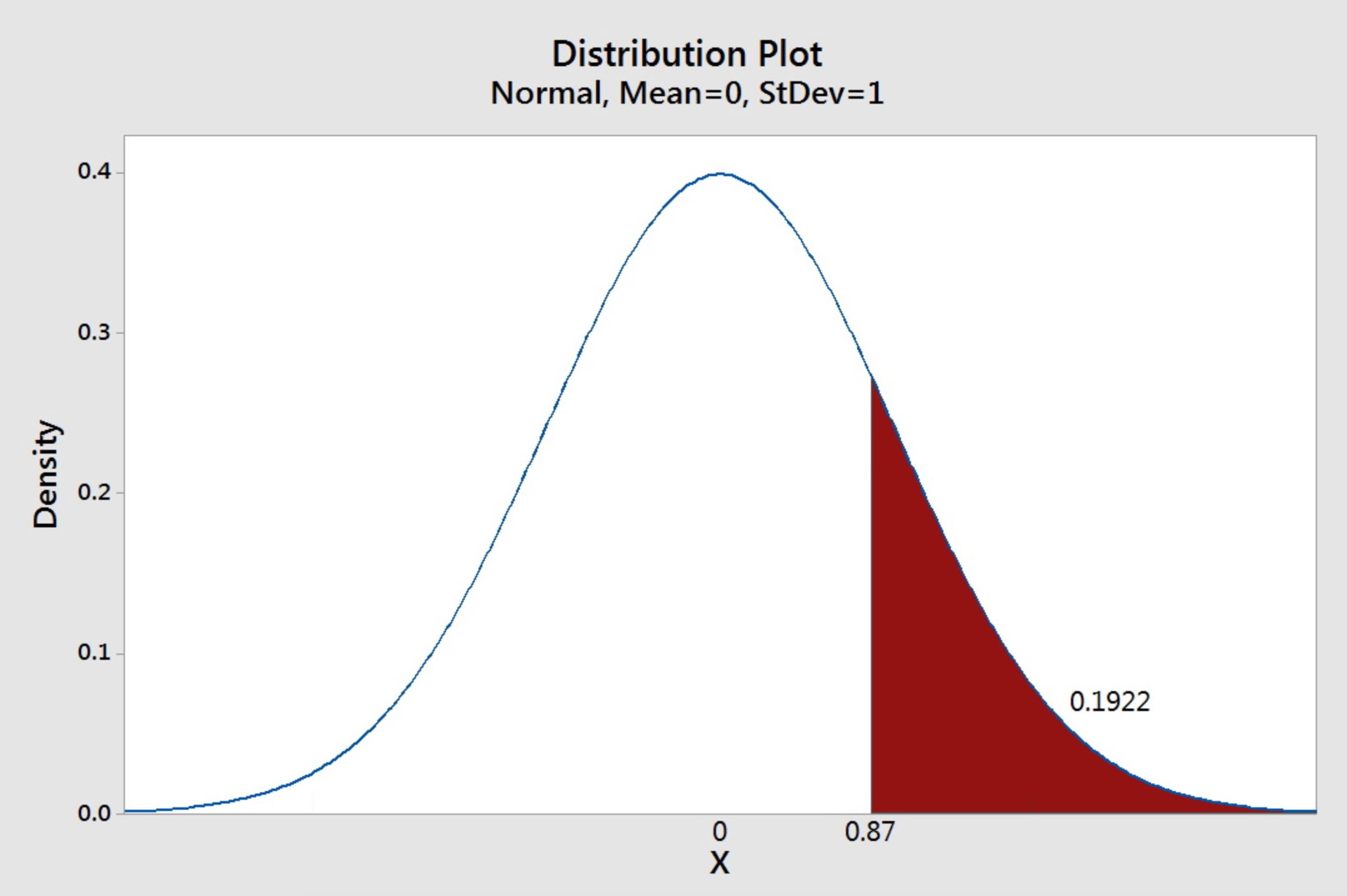
Find the area nether the standard normal curve to the right of 0.87.

• Method one: Using a table
• Method 2: Using Minitab

Based on the definition of the probability density function, we know the area nether the whole curve is i. Since we are given the "less than" probabilities in the table, we can use complements to find the "greater than" probabilities. Therefore,

\(P(Z>0.87)=ane-P(Z\le 0.87)\).

Using the data from the last example, we take \(P(Z>0.87)=ane-P(Z\le 0.87)=ane-0.8078=0.1922\)

Using Minitab

Since nosotros are given the "less than" probabilities when using the cumulative probability in Minitab, we can employ complements to find the "greater than" probabilities. Therefore,

\(P(Z>0.87)=1-P(Z\le 0.87)\).

Using the data from the last example, we have \(P(Z>0.87)=ane-P(Z\le 0.87)=1-0.8078=0.1922\)

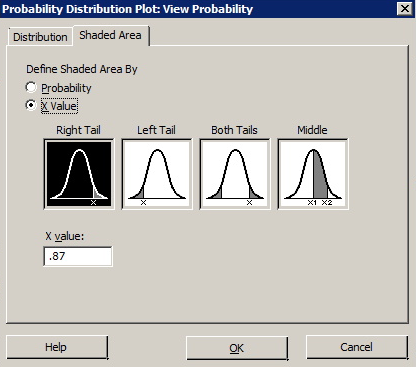
You can also use the probability distribution plots in Minitab to find the "greater than."

1. Select Graph> Probability Distribution Plot> View Probability and click OK.
2. In the pop-up window select the Normal distribution with a mean of 0.0 and a standard deviation of 1.0.
3. Select the Shaded Area tab at the top of the window.
4. Select X Value.
5. Enter 0.87 for 10 value.
6. Select Right Tail.
7. Click OK.

Example 3-xi: Probability 'betwixt' Department

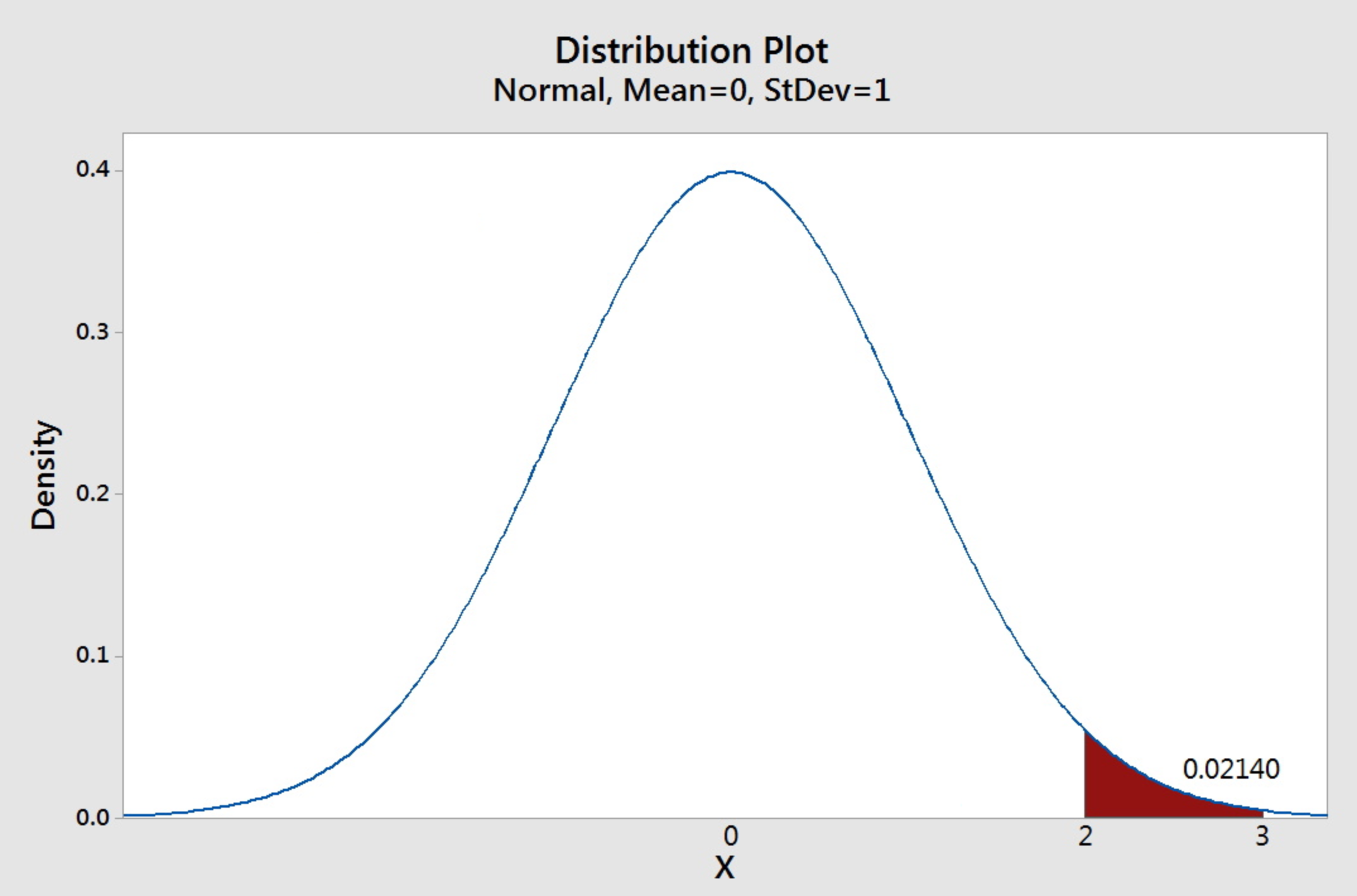
Notice the area nether the standard normal curve betwixt 2 and 3.

• Method one: Using a table
• Method 2: Using Minitab

To notice the probability betwixt these two values, subtract the probability of less than 2 from the probability of less than 3. In other words,

\(P(2<Z<3)=P(Z<3)-P(Z<2)\)

\(P(Z<3)\) and \(P(Z<ii)\) tin can be found in the table by looking up 2.0 and 3.0.

For 3.0...

z	.00	.01	.02	.03	.04	.05	.06	.07	.08	.09
2.8	0.9974	0.9975	0.9976	0.9977	0.9977	0.9978	0.9979	0.9979	0.9980	0.9980
two.9	0.9981	0.9982	0.9982	0.9983	0.9984	0.9984	0.9985	0.9985	0.9986	0.9986
3.0	0.9987	0.9987	0.9987	0.9988	0.9988	0.9989	0.9989	0.9989	0.9990	0.9990
3.one	0.9990	0.9991	0.9991	0.9991	0.9992	0.9992	0.9992	0.9992	0.9993	0.9993

For 2.0...

z	.00	.01	.02	.03	.04	.05	.06	.07	.08	.09
1.8	0.9641	0.9649	0.9656	0.9664	0.9671	0.9678	0.9686	0.9693	0.9699	0.9706
i.ix	0.9713	0.9719	0.9726	0.9732	0.9738	0.9744	0.9750	0.9756	0.9761	0.9767
2.0	0.9772	0.9778	0.9783	0.9788	0.9793	0.9798	0.9803	0.9808	0.9812	0.9817
2.1	0.9821	0.9826	0.9830	0.9834	0.9838	0.9842	0.9846	0.9850	0.9854	0.9857

\(P(ii < Z < 3)= P(Z < 3) - P(Z \le  2)= 0.9987 - 0.9772= 0.0215\).

Using Minitab

To notice the surface area between ii.0 and 3.0 nosotros can employ the calculation method in the previous examples to find the cumulative probabilities for 2.0 and 3.0 and and so subtract.

\(P(2 < Z < iii)= P(Z < 3) - P(Z \le  2)= 0.9987 - 0.9772= 0.0215\)

Yous tin can also utilise the probability distribution plots in Minitab to observe the "between."

1. Select Graph> Probability Distribution Plot> View Probability and click OK.
2. In the popular-up window select the Normal distribution with a mean of 0.0 and a standard deviation of one.0.
3. Select the Shaded Expanse tab at the peak of the window.
4. Select X Value.
5. Select Heart.
6. Enter ii.0 for Ten value 1 and 3.0 for X value 2.
7. Click OK.

Percentiles of the Standard Normal Distribution Section

Recall from Lesson 1 that the \(p(100\%)^{th}\) percentile is the value that is greater than  \(p(100\%)\) of the values in a data gear up. We can use the standard normal table and software to find percentiles for the standard normal distribution.

The intersection of the columns and rows in the tabular array gives the probability. If we look for a detail probability in the table, we could so find its corresponding Z value.

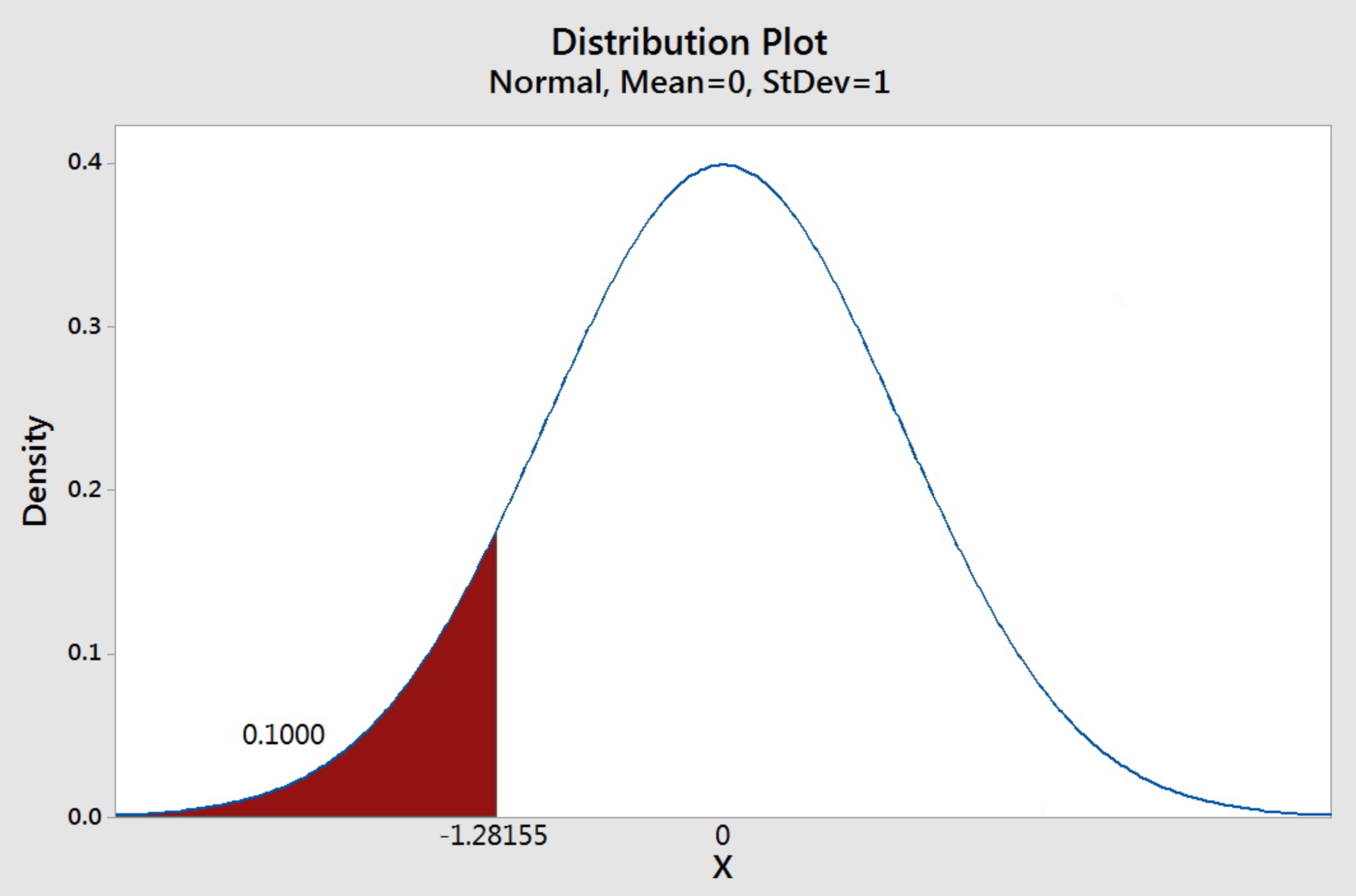
Example three-12: Percentiles in the Standard Normal Distribution Section

Detect the tenth percentile of the standard normal curve.

• Method 1: Using a table
• Method ii: Using Minitab

The question is asking for a value to the left of which has an area of 0.1 under the standard normal bend.

Since the entries in the Standard Normal Cumulative Probability Table represent the probabilities and they are four-decimal-identify numbers, we shall write 0.1 as 0.m to remind ourselves that it corresponds to the inside entry of the tabular array. Nosotros search the body of the tables and detect that the closest value to 0.thousand is 0.1003. We expect to the leftmost of the row and up to the top of the column to notice the corresponding z-value.
The respective z-value is -1.28. Thus z = -ane.28.

z	.00	.01	.02	.03	.04	.05	.06	.07	.08	.09
-1.iii	0.0968	0.0951	0.934	0.0918	0.0901	0.0885	0.0869	0.0853	0.0838	0.0823
-ane.2	0.1150	0.1131	0.1112	0.1093	0.1075	0.1056	0.1038	0.1020	0.1003	00985
-1.1	0.1357	0.1335	0.1314	0.1292	0.1271	0.1251	0.1230	0.1210	0.1190	0.1170
-ane.0	0.1587	0.1562	0.1539	0.1515	0.1492	0.1469	0.1446	0.1423	0.1401	0.1379

Therefore, the 10th percentile of the standard normal distribution is -1.28.

Using Minitab

To observe the 10th percentile of the standard normal distribution in Minitab...

1. Select Calc> Probability Distributions> Normal.
2. In the new window choose Inverse Cumulative Probability.
3. Enter 0.1 in the Input constant box.
4. Click OK.

You should run across a value very close to -1.28.

blumtwome1964.blogspot.com

Source: https://online.stat.psu.edu/stat500/lesson/3/3.3/3.3.2

Share this post